Abstract
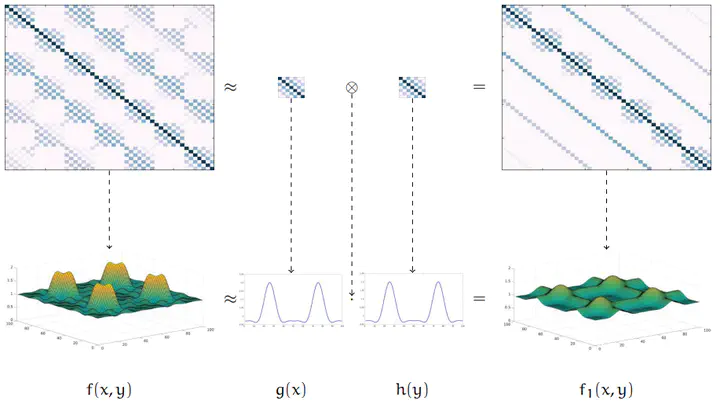
The metrology of integrated circuits (ICs) requires multiple solutions of a large-scale linear system. The time needed for solving this system, greatly determines the number of chips that can be processed per time unit. Since the coefficient matrix is partly composed of block-Toeplitz-Toeplitz-block (BTTB) matrices, approximations of its inverse are interesting candidates for a preconditioner. In this work, different approximation techniques such as an approximation by sums of Kronecker products or an approximation by inverting the corresponding generating function are examined and where necessary generalized for BTTB and BTTB-block matrices. The computational complexity of each approach is assessed and their utilization as a preconditioner evaluated. The performance of the discussed preconditioners is investigated for a number of test cases stemming from real life applications.
Frank Schneider
Postdoctoral Researcher
I am a postdoc in the Methods of Machine Learning group at the University of Tübingen working on training methods for deep learning.