Inverse generating function approach for the preconditioning of Toeplitz-block systems

Abstract

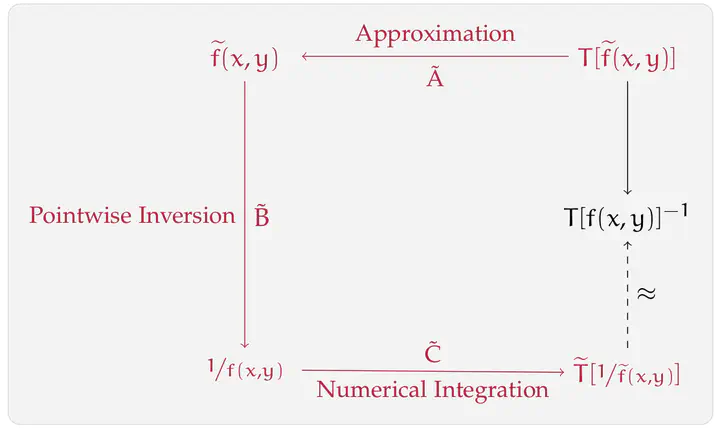
As proposed by R. H. Chan and M. K. Ng (1993), linear systems of the form $T[f]x=b$, where $T[f]$ denotes the n×n Toeplitz matrix generated by the function $f$, can be solved using iterative solvers with $T[ \frac{1}{f}]$ as a preconditioner. This article aims at generalizing this approach to the case of Toeplitz‐block matrices and matrix‐valued generating functions $F$. We prove that if $F$ is Hermitian positive definite, most eigenvalues of the preconditioned matrix $T[F^{-1}]T[F]$ are clustered around one. Numerical experiments demonstrate the performance of this preconditioner.